Introduction
2進数から8進数に変換する方法を説明します。
情報の基数変換の問題としては、2進数、10進数、16進数の相互変換がおきまりなのですが、少しひねった問題として8進数も稀に出題されることがあります。

8進数への変換は、16進数への変換方法と考え方が似ているよ
ちなみに、1桁に8種類の文字を使うのが8進数です。
下の10進数との対応表を見ると、8進数の仕組みが分かり易いと思います。
| 10進数 | 8進数 |
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 10 |
| 9 | 11 |
| 10 | 12 |
| 11 | 13 |
| 12 | 14 |
| 13 | 15 |
| 14 | 16 |
| 15 | 17 |
| 16 | 20 |
ポイントは1桁で「7」より大きい数字は扱えないので、すぐに桁が上がるところですね。
変換方法は2進数を10進数へ変換するやり方が元となります。不安な方は先に下のリンク先をご覧ください。

また、考え方は2進数を16進数に変換する方法と同じです。

それぞれを理解しておくと、8進数の変換は簡単に感じるはずですよ。

8進数と16進数は考え方が似ているよ
2進数から8進数に変換する方法
では、変換の方法を説明していきます。
例として下の2進数を8進数に変換してみます。
(10100110)2
※2進数の表記方法や、2進数そのものの意味を知りたい方はこちらを先にご覧ください。
2進数を8進数に変換するには、下の4つの手順を踏みます。
- 3ビット(3桁)ずつに分けて線を引く
- 分けた3ビットごとに2進数の上に20から順番に記入していく
- 2進数の「1」が存在する場所だけ計算結果を下に書く
- 3ビットずつ、下に書いた計算結果を合計したものが8進数の1桁になる。
文字で説明すると長くなりますね・・・。
しかし、手順は2進数を10進数へ変換する方法さえ覚えていれば簡単です。
では、順番にやってみましょう。

まず、3ビットごとに縦に線を引きましょう。
今回の例は8ビットなので、2本引く必要があります。

そして、2進数から10進数へ変換する時と同じように、
右から「20」「21」「22」の並びを、繰り返し記入していきます。

そして、「1」のある場所だけ上に書いた2の累乗の計算を行い、結果を下に記入しましょう。
※累乗・・・同じ数を繰り返し掛け算すること

その計算結果を、3ビットずつ合計したものが、8進数の1桁になります。
※今回の例では、合計する必要があるのは1番右の桁だけです。
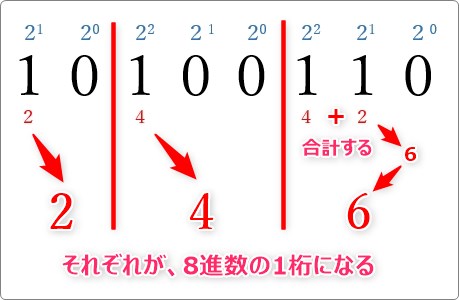
今回の場合は、 (246)8 が8進数に変換した数値になります。
では、もう一つやってみて手順を復習しましょう。
今度は、下の (1101110)2 を8進数に変換してみます。

まず、3ビットの場所で縦線を引いておきます。

そして、上に「20」「21」「22」と順番に振って、
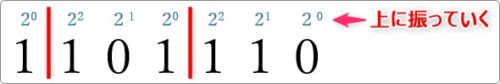
「1」のある場所だけ下に計算結果を記入します。

最後に、計算結果を足し算して、3ビットごとに下に並べましょう。
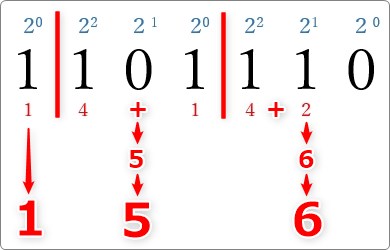
8進数に変換した結果は (156)8 になります。
なぜ3ビットずつ処理すると8進数に変換できるんだろう?
その理由を続けて説明します。
変換方法の仕組み
まず、「8進数」とはどういうものかを考えます。
「1桁で8種類の文字を使って良いのが8進数」でした。
「01234567」・・・全部で8種類
この事に関しては、下のリンク先で説明しています。

言葉を変えると、8進数とは、1桁で8種類の大きさを表現できることになります。

そして、今度は2進数を考えてみましょう。
2進数3桁、つまり3ビットで表現できる数はいくつか考えます。
「nビットで表現できる数は2のn乗になる」・・・詳しい説明はこちら
3ビットの場合は23になりますね。
23 = 8
つまり、2進数は3ビットで8の大きさを表現できることになります。

お! 8!
ということは、3ビットで8進数の1桁を表現できますね。
下のイメージです。
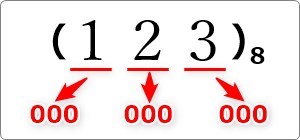
「8進数の1桁は2進数の3桁で表示することができる」
このことを理解することが大切です。
そう考えると8進数と2進数は仲良しな気がしますね。
覚えておくべきポイント
2進数から8進数へ変換する際に覚えておくべきポイントをまとめておきます。
3ビットずつで考える
2進数3桁(3ビット)が8進数の1桁になることを理解することが大切。

3ビットごとに2の0乗からスタートする
「20」「21」「22」の次は、また「20」からスタートすることを忘れずに。
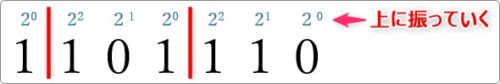
練習問題
◎ 各問題をクリック(タップ)すると答えが出てくるよ

2進数の3桁が8進数の1桁か。

2進数と8進数は仲が良いみたいだね。

