２進数で表現できる数は２の累乗になるとは、どういう意味なの？

Introduction

２進数を学習すると必ず出てくる「２進数は２の累乗になる」「nビットは２のn乗になる」という言葉。この意味をスッキリさせましょう。

• ２進数で表現できる数は２の累乗になる
• nビットで表現できる数は２のn乗になる

この２つの説明の内容は同じです。

今回の説明を読んだ後に、この場所に戻ってきてください。

上の２つの意味が「確かにそうだねー」となったらバッチリ理解したことになります。

この場所を学習する前に、２進数を理解しておく必要があります。

下のリンク先で説明しています。

コンピューターで扱う２進数とは何？ーその意味を分かり易く説明しますー

コンピューターで扱う２進数とはどのようなものでしょうか。文系の方でも理解しやすいように、なるべく簡単にわかりやすく説明してみます。

prau-ict.com

 

２進数で表現できる数は２のn乗になる

まず、２進数の１桁を１ビットと呼ぶ事を再確認。

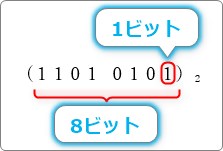
上の画像の場合は８ビット存在することになります。

 

では、話を進めていきます。

２進数１桁（1ビット）で表現できる組み合わせはいくつあるでしょうか？

１桁につき「０」と「１」が使えるので、

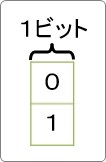
２つですね。

※表現できる最大値としては「１」ですが、組み合わせとして考えると「０」と「１」の２種類です。

 

では、続いて２進数２桁（２ビット）ではどうでしょう。

「０」と「１」がつ使える２桁の組み合わせになります。

００
０１
１０
１１

ということで、下の画像のように異なる４つの組み合わせが可能ですね。

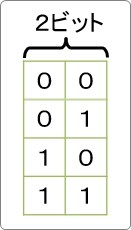
３桁（３ビット）ではどうでしょう。

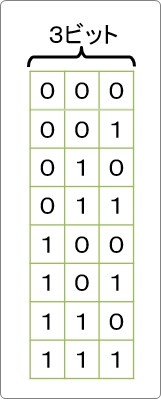
３ビット使用するとかなり多くの組み合わせが可能ですね。

８つもできました。

もう一ついきましょう。

４桁（４ビット）使うとどうなるか・・・。

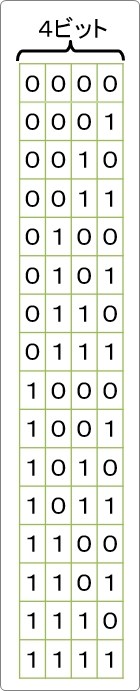
16の組み合わせが可能です。一気に増えました。

ここまでの結果をまとめると下のようになります。

1桁（1ビット）・・・2

2桁（2ビット）・・・4

3桁（3ビット）・・・8

4桁（4ビット）・・・16

使用できる桁数（ビット数）が増えると、表現できる組み合わせの数がどんどん増えていきますね。

ここで良く見ると、規則性があるのに気づきます。

2　→　4　→　8　→　16

ん？　２倍ずつ増えている。

 

つまり、下図のように１桁（１ビット）増えると、表現できる数（組み合わせ）は２倍ずつ増えていることが分かります。

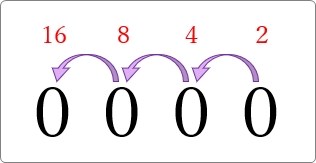
それぞれを式で表すと　2¹、2²、2³、2⁴になりますね。

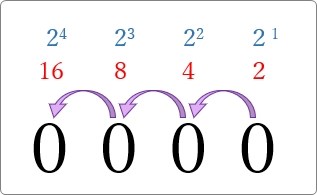
うん。２の累乗で増えていくことが確認できました。
※累乗・・・同じ数を繰り返し掛け算すること

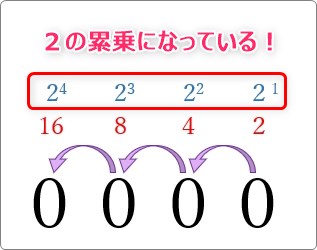
言葉にすると、

これは、この説明の最初に書いた言葉です。

同じ説明をもう少し噛みくだいて言うと、

と言うことですね。

また、同じ内容をビット単位で考えると、

ということになります。

 

 

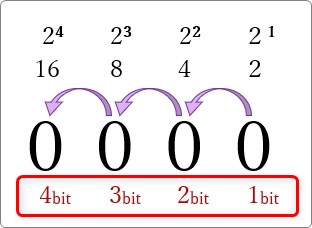
続けて下の画像を見てください。

先ほどの画像の下に、使用しているビット数を付けたものです。

赤丸部分に注目です。

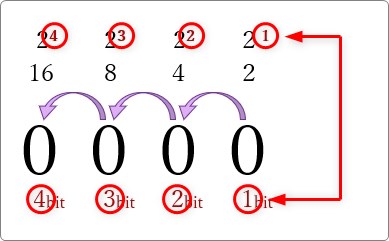
使用しているビット数と２^〇部分が同じ数字になっています。

このことから「〇ビットで表現できる数は２の〇乗になっている」ことが分かります。

この言葉の「〇」を「n」に置き換えると

となります。

１ビットだと２^１・・・２
２ビットだと２^２・・・４
３ビットだと２^３・・・８
４ビットだと２^４・・・１６

というように、表現できる数（組み合わせ）が増えていくということです。

 

nビットで表現できる数は2のn乗になる

これを覚えておくと、下のような問題は即答できるようになります。

nビットで表現できる数は2のn乗になる

↓

８ビットで表現できる数は２の８乗になる

２^８＝　256

となります。

練習問題

◎ 各問題をクリック(タップ)すると答えが出てくるよ