Introduction
これまで説明した論理回路を使用した例として、半加算回路と全加算回路を紹介します。
まだ、論理回路の説明をご覧になっていない方は先に下のリンク先を読んでいただくのがお勧めです。
また、2進数の足し算を思い浮かべると理解しやすくなります。
半加算回路とは、1桁の足し算ができる回路です。
全加算回路とは、2桁以上の足し算もできる回路。桁上げされた数値まで考慮します。
それぞれ回路の説明でよく使われるのでしっかり理解しておくのがおすすめです。
回路の組み合わせと真理値表の両方を見比べながら学習しよう！
半加算回路
半加算回路とは、1ビットの足し算ができる回路のことです。
回路をみる前に、1ビットの足し算を復習しておきましょう。
- 0+0 → 0
- 0+1 → 1
- 1+0 → 1
- 1+1 → 0・・・桁上がり「1」
となりますね。下の図を見てもらった方がピンとくるかもしれません。
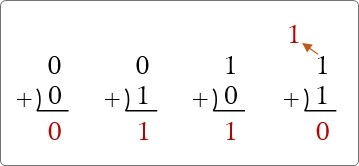
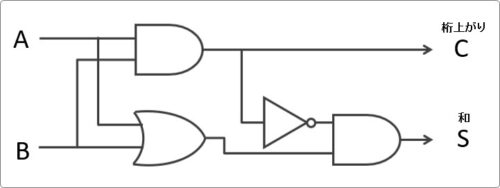
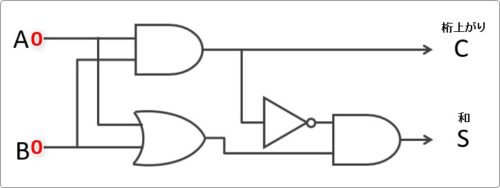
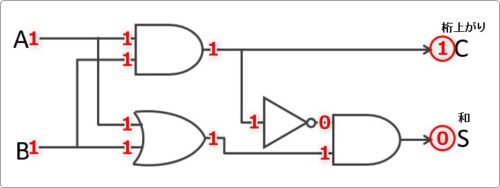
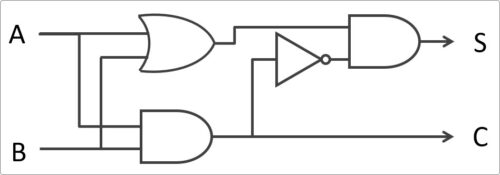
これを回路で実現すると下の図のようになります。
「A」「B」の値が入力されると、足された結果が「S」となり、桁上がりの結果が「C」となります。
※今回の説明では、入力に「Ａ」「Ｂ」、出力に「Ｓ」「Ｃ」というアルファベットを使用していますが特に決まりはありません。
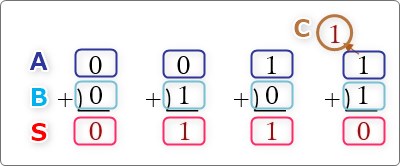
先ほどの足し算の図を「A」「B」「S」「C」に分けると下図になります。
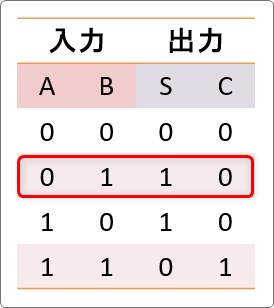
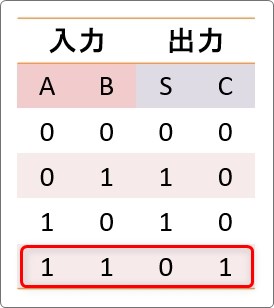
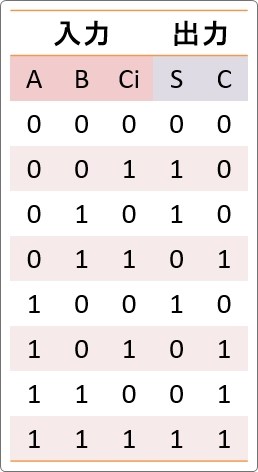
そして真理値表がこちら。
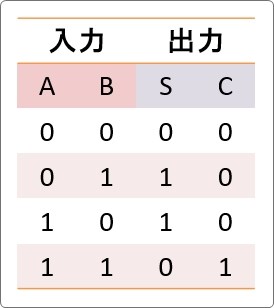
では、本当にそうなるのか「A」「B」に「0」と「1」を入力して出力まで追っかけていきましょう。
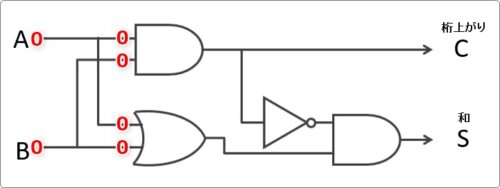
まず、「A」も「B」も「0」だった時の出力を確認します。
そのまま最初の回路の入り口まで「0」を伸ばしていきます。
上はAND回路、下はOR回路を通過します。
どちらも「0」が入力されると「0」が出てくるので、回路を出た後の結果は下のようになります。
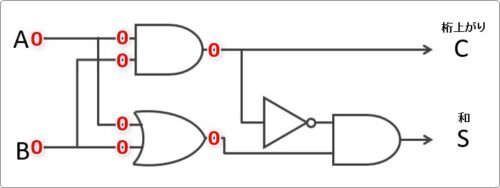
桁上がりの場所はそのまま「0」が出力となります。
下の方へ移動していくと、NOT回路があります。
ここで初めて出力結果に「1」が登場！
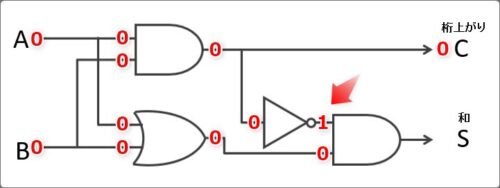
でもその後のAND回路の結果、「0」に戻って和は「0」になります。
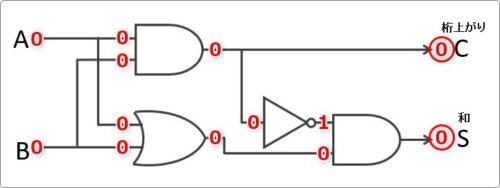
ということで「A」「B」に「0」が入力された際の「C」「S」の出力は両方「0」となりました。
先ほどの真理値表の一番上です。
確かにそうなっていますね。
次に「A」に「0」、「B」に「1」が入力された際を追いかけていきましょう。
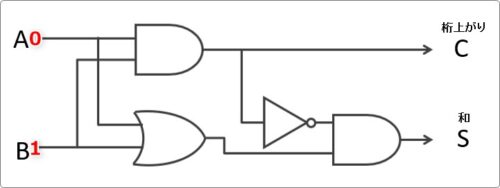
どんどん追っかけていくよー
まず「0」と「1」を回路の前に移動して・・・。
それぞれの回路を通過した結果は「0」と「1」になります。
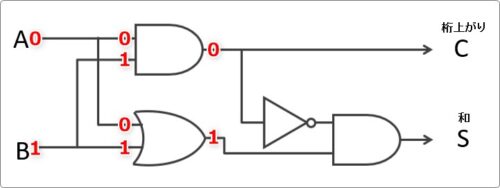
上のAND回路の結果「0」は、そのまま「桁上がり」の結果になりますね。
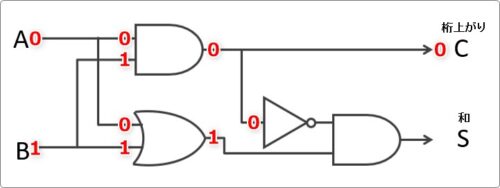
下の場所はNOT回路の場所で「0」が「1」になるので、「1」と「1」がOR回路に入力されて・・・。
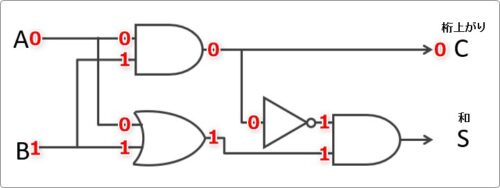
和の場所は「1」が出力されます。
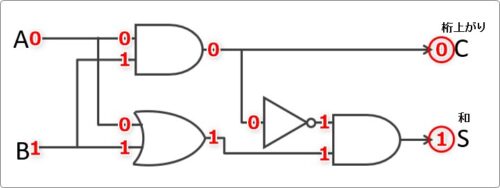
ということで、「A」に「0」、「B」に「1」が入力された際の出力は、「C」が「0」、「S」は「1」となりました。
先ほどの真理値表の２番目です。
次の「A」に「1」、「B」に「0」が入力された際は飛ばします。
最後に「A」「B」両方に「1」が入力されたパターンを追いかけていきましょう。
ここだけ桁上がりの「C」に「1」が出力されるはずです。
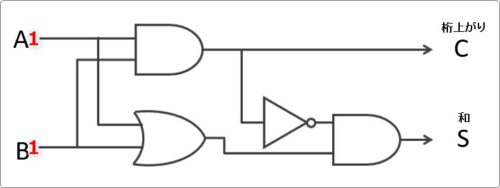
まず「1」を回路の前に移動して、
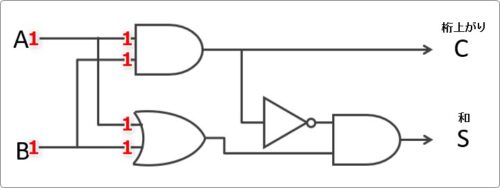
その出力結果を書いて、
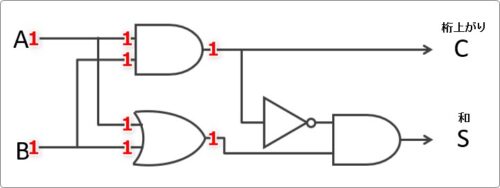
うん。確かに桁上がりは「1」になりますね。
さらに下の回路の入出力を追いかけていくと、
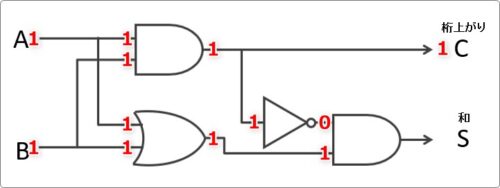
和は「0」になります。
真理値表と同じ出力になりました。
いかがでしたか？
以上のように1桁の2進数の結果が再現されていますね。
これを半加算回路とよんでいます。
半加算回路は有名なので、丸暗記してしまっても良いかもしれません。
また、半加算回路が提示されて、対応した真理値表の空欄を埋める問題も見かけます。
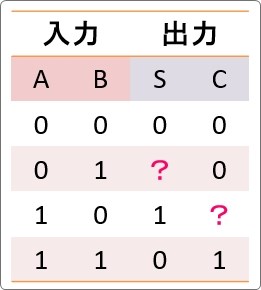
各回路の入出力結果を正確に覚えておきたいですね。
全加算回路
半加算回路は1桁の足し算しか考えられていません。
2桁以上の足し算をするには、もう一つ必要な情報が増えます。
その情報とは、下の桁からの桁上げされた値です。
入力すべき値が1つ増えます。
下の図で言うと、上部の赤字の部分です。
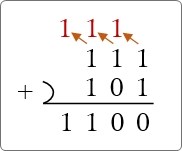
2桁目の「入力を赤枠」「出力を青枠」で囲んでみたのが下の画像です。
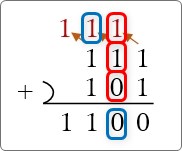
それぞれを説明すると下のようになります。
「A」に「1」、「B」に「0」が入力されるだけではなく、さらに「Ci」に前の桁からの繰り上がりの「1」も入力されます。
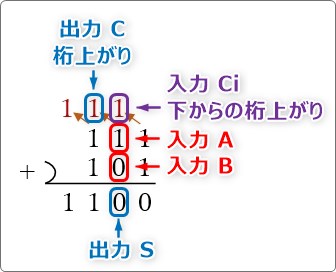
出力は、先ほどの半加算回路と同じです。
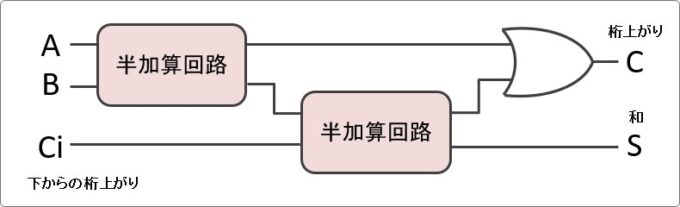
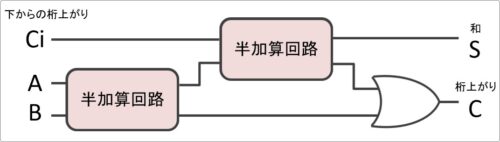
そして、その全加算回路は下図のようになります。
途中で先ほど説明した「半加算回路」を使用しています。
また、入力が半加算回路より１つ増えていますね。下からの桁上がりです。
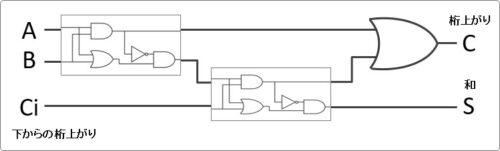
半加算回路を無理やりはめ込んだのが下の画像です。
雰囲気がつかめるかもしれません。
その真理値表が下の図です。
入力が3つになったため組み合わせが増えます。
こちらを、先ほどの半加算回路のように入力結果を追いかけると大変なのでやりません。
もし時間があれば試してみてください。
覚えておくべきポイント
- 基本回路の動きはしっかり覚えておこう
- 回路の入力 → 出力結果を順番に追いかけられるようにしておこう
- 余力があれば半加算回路と全加算回路の全体を覚えてしまおう
- ここで説明した回路図は、それぞれ上下反転していることもあります。
練習問題
◎ 各問題をクリック(タップ)すると答えが出てくるよ
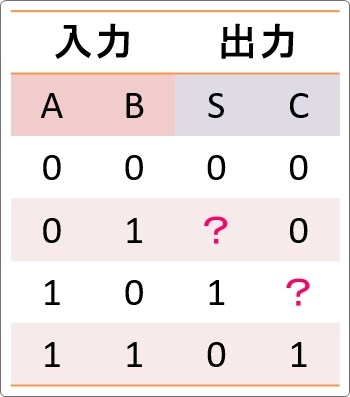「S」・・・1 「C」・・・0
AND回路やOR回路を組み合わせることで色んな計算ができるんだね