Introduction
8進数から2進数に変換する方法を説明します。
やり方を覚えてしまえば変換は簡単に行うことができます。
変換方法は途中で10進数を2進数へ変換するやり方を使用します。不安な方は下のリンクを先にご覧ください。

最初にやり方を簡単に説明して、次になぜその方法で変換できるのかを説明します。

10進数から2進数への変換方法を使うよ
8進数から2進数に変換する方法
最初に変換の流れを書いておきます。
- 8進数を1桁ずつに分ける
- 分けた8進数1桁をそれぞれ2進数へ変換する
- 変換した2進数を順番に並べる
では、やっていきましょう。
例として、(63)8を変換してみます。

方法としては、8進数の1桁をそれぞれ3ビットの2進数へ変換していきます。
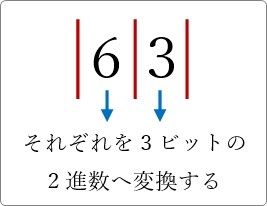
1桁ずつ考えていくので、線を引くとイメージしやすいでしょう。
各桁の数字を2進数へ変換していきます。
「2」で割り算して、余りを右に書いて、その余りを下から並べれば2進数への変換終了です。
※この変換(10進数から2進数への変換)が不安な方はこちらをどうぞ。
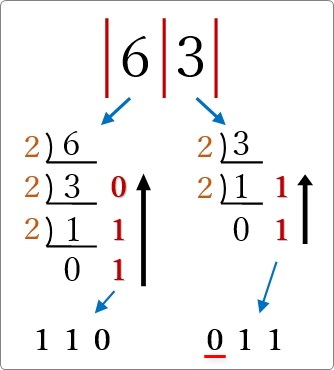
1桁目の「3」は (11)2 になるのですが、(011)2 と表記しています。
理由は、8進数の一桁は、2進数3ビット分の大きさがあるためです。
この後でもう少し詳しく説明しますが、
と覚えておくと安心です。
そして、それをくっ付けて順番に並べると2進数への変換終了です。
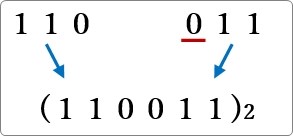
この流れを一つの画像にまとめると下のようになります。
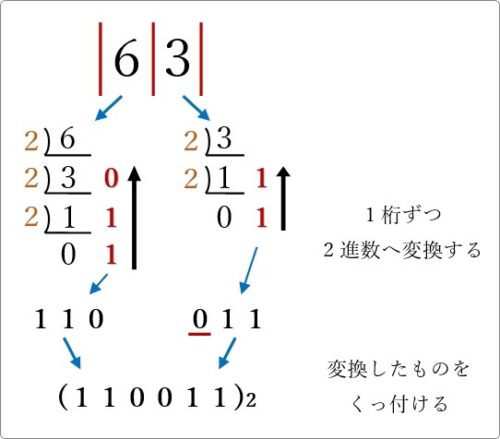
では、なぜこの方法で8進数を2進数へ変換できるのでしょうか。
理由は、8進数がどのようなものかを考えると納得できるはずです。
1桁で8種類の大きさを表現できるのが8進数
下の表を見ると、1桁で0~7までの8種類の大きさを表すことができているのが分かります。
※最大値は「7」になりますが、「0」を含めると「8」種類の大きさを表しています。
※8進数の説明はこちら。
| 10進数 | 8進数 |
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
| 7 | 7 |
| 8 | 10 |
| 9 | 11 |
| 10 | 12 |
| 11 | 13 |
| 12 | 14 |
| 13 | 15 |
| 14 | 16 |
| 15 | 17 |
| 16 | 20 |
「1桁で8種類」
これを覚えておいて2進数へ話を移動します。
2進数3桁(3ビット)で表現できる数はいくつでしたっけ?
※この説明はこちらで詳しく説明しています。
ということで、3ビットで表現できる数は2の3乗
23 = 8
になります。
8!!
- 2進数3桁(3ビット)で表現できる数は「8」。
- 8進数の1桁では「8」種類表現できる。
同じ8ですね。
そうなると、8進数の1桁は2進数3桁で置き換えることができる!

8進数と2進数は仲が良いと言えますね。

では、もう1問練習しておきましょう。
次は
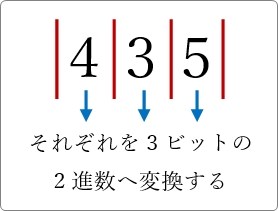
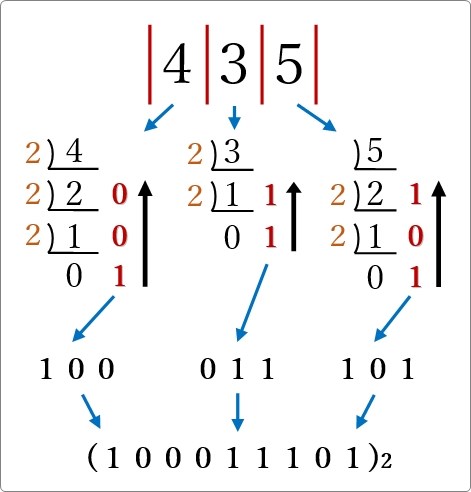
(435)8
を変換してみます。

それぞれの桁を2進数の3ビット分へ変換していきます。
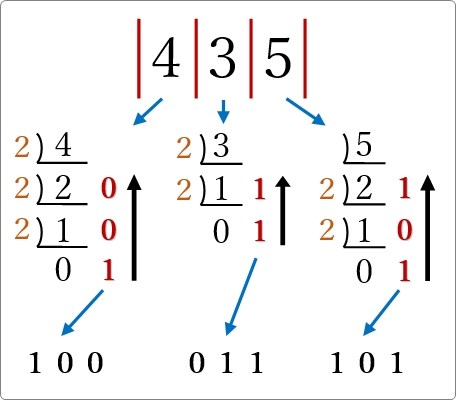
各桁を「2」で割って、余りを右に書いて、下から並べます。
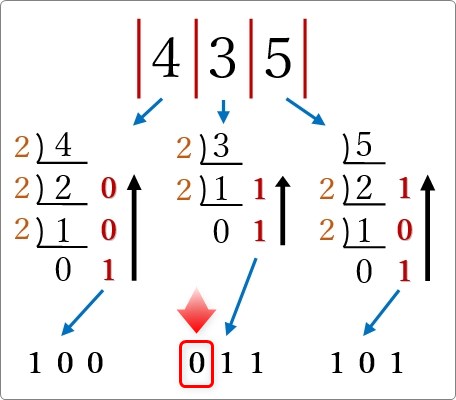
2桁目の「3」を変換する際に注意が必要です。
変換すると (11)2 となりますが、3ビットとして考えるので (011)2 と3ビットになるように左を「0」で埋めましょう。
そして、それらをくっ付ければ変換終了です。
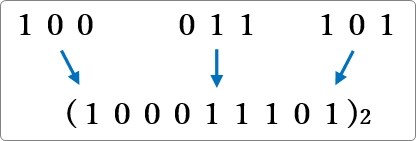
全体をまとめると下のようになります。
どうでしょう。
慣れてきましたか?
覚えておくべきポイント
- 8進数の1桁を、2進数3桁に変換する
- それぞれの桁の変換は10進数への変換方法と同じ
- 次の左の桁が存在しているのに3桁にならない時は「0」で埋めて3桁にする
例: (1)2 → (001)2 (10)2 → (010)2
練習問題
◎ 各問題をクリック(タップ)すると答えが出てくるよ

8進数の1桁を2進数の3桁で表現できるのか

「n進数」の意味を考えると分かり易いかもね

