２進数から１０進数に変換する方法｜やり方を簡単に分かりやすく解説します

Introduction

２進数から１０進数に変換する方法を説明します。

機械的に覚えてしまうのも良いのですが、その仕組みを理解しておくと応用が効きます。

そのため、最初にやり方を説明してから次になぜその方法で可能なのかを説明していきます。

 

 

この場所を学習する前に、２進数を理解しておく必要があります。

下のリンク先で説明しています。

コンピューターで扱う２進数とは何？ーその意味を分かり易く説明しますー

コンピューターで扱う２進数とはどのようなものでしょうか。文系の方でも理解しやすいように、なるべく簡単にわかりやすく説明してみます。

prau-ict.com

 

２進数から１０進数に変換する方法

では、早速変換方法を説明していきます。

例として下の２進数を１０進数に変換してみます。

(10100110)₂

※２進数の表記方法や、２進数そのものの意味を知りたい方はこちらを先にご覧ください。

２進数を１０進数に変換するには、下の３つの手順を踏みます。

1. ２進数の上に2⁰から順番に記入していく
2. ２進数の「1」が存在する場所だけ計算して下に書く
3. 下に書いた計算結果を合計する

 

では、順番にやってみましょう。

まず、変換したい２進数の上に右から「２^０」「２^１」「２^２」というように順番に振っていきます。

そして、「１」のある場所だけ今記入した２の累乗の計算を行い、結果を下に記入しましょう。
※累乗・・・同じ数を繰り返し掛け算すること

最後に計算した結果を合計します。

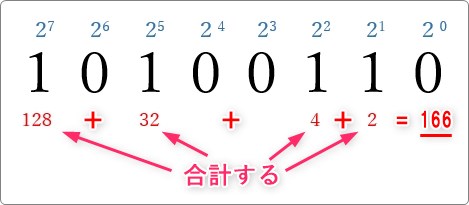
今回の場合は「166」が10進数に変換した数字になります。

 

では、もう一つやってみて手順を復習しましょう。

今度は、下の　(11001)₂　を１０進数に変換してみます。

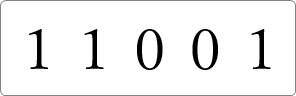
まず、上に「２^０」「２^１」「２^２」と順番に振って、

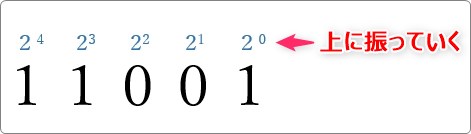
「1」のある場所だけ下に計算結果を記入します。
※２^０は「1」です。

最後に、計算結果を足し算して終了。

どうやら「25」のようですね。

 

慣れてくると、上に「２^０」「２^１」「２^２」と記入していかなくても直接下に計算結果を記入できるようになりますよ。
※「1」のある場所だけ2の累乗を下に記入すればOK。

とりあえず、この方法で簡単に変換はできます。

では、なぜこの方法で変換できるのか。その理由を続けて説明します。

変換方法の仕組み

まず、下の２進数と１０進数の対応表をご覧ください。

ごく普通の対応表です。

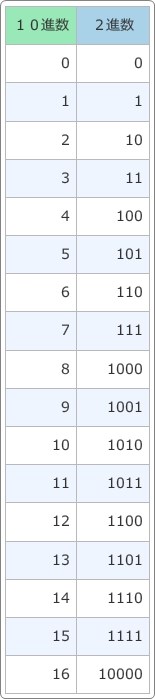
この表の赤丸を付けた場所に注目です。

赤丸を付けた場所は、「1」が一つだけの場所です。

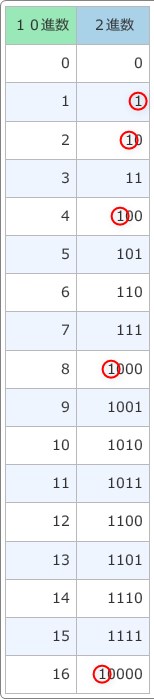
上から順番に並べると

となります。

最初を除き、桁が上がった場所ですね。

新しく桁が上がると、左側に「1」が登場し、右側は「0」に戻ります。
つまり、その桁にだけ「1」が存在する場所。
※右側を見ると「0」しか存在していませんね。

言葉を変えると、「その桁だけの大きさを表している」ということになります。

そして、その場所の１０進数を確認してください。

この場所をまとめると、

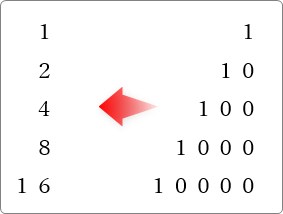
となっています。

気付きましたか？

左側１０進数の「１」「２」「４」「８」「１６」ですが、

これは「２^０」「２^１」「２^２」「２^３」「２^４」になっているのです。

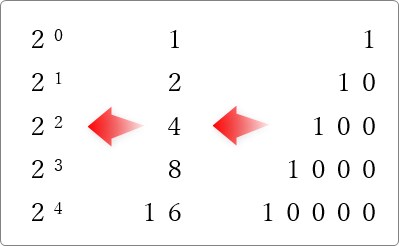
つまり、それぞれの桁の「1」の場所は下画像のような大きさを持っているということ。

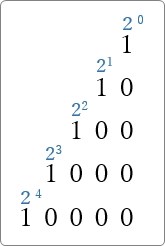
「0」を省いて横に並べると下画像のようになります。

これって、２進数を１０進数へ変換する時に、「最初に上に記入しましょう」と言ったものですね。

そして「「1」のある場所だけ計算して後で足し算」でした。

 

 

それぞれの桁の大きさは２の累乗になっていて、桁に数値が存在する（1がある）場所だけ足し算すれば１０進数に変換できるということです。

 

どうでしょうか。スッキリしたでしょうか。

「いまいちピンとこない」という方は、もう一度ゆっくり読み直してみてください。

「あ！なるほど！」となれば２進数を理解するコツをつかんだ事になりますよ。

ｎビットでの最大値は２n-1になる

情報で２進数を学習する際に必ず出てくる「nビットでの最大値は2ⁿ-1」になるという言葉。

その意味をここで説明しておきたいと思います。

まず、２進数の１桁を１ビットと呼ぶ事を再確認。

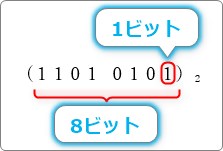
上の画像の場合は８ビット存在することになります。

つまり、下の２つは同じ意味です。

• nビットでの最大値は2ⁿ-1
• 2進数n桁での最大値は2ⁿ-1

 

文系で「n」やら「x」「y」が嫌いな方は、適当な数値を当てがって想像しましょう。

• nビットでの最大値は2ⁿ-1　→　4ビットでの最大値は2⁴-1

のように具体的な数値を入れてあげるとイメージが固まります。

「使用したビット数（2進数の桁数）の回数ぶん「2」を掛け算したものから「1」引けば最大値になるんだ」

というイメージです。

 

 

では、いきましょう。

実際に１ビット（2進数1桁）ごとの最大値を計算してみます。

まず1ビット（2進数1桁）の場合。

最大値は「1」ですね。

次に2ビット（2進数2桁）の場合。
※全て「1」が並んだ状態が最大値になります

「3」ですね。

次に3ビット（2進数3桁）の場合。

「7」ですね。

もう一ついきましょうか。

4ビット（2進数4桁）の場合。

「15」です。

ここまでの結果を並べると、

「1」「3」「7」「15」

になりますね。これが各ビットまでを使用した最大値です。

上には、それぞれのビット数だけ2を累乗した結果を記入してみます。

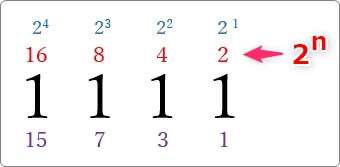
最大値と比べてみると・・・。

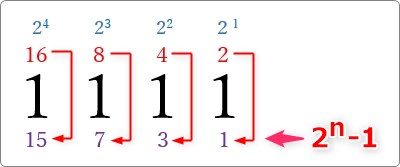
毎回「2ⁿ」から「1」引いた数字になっていますね。

 

 

• nビットでの最大値は2ⁿ-1になる
• 2進数n桁での最大値は2ⁿ-1になる

という事が確認できました。

覚えておくべきポイント

2進数から10進数へ変換する際に覚えておくべきポイントをまとめておきます。

1桁目を見れば偶数か奇数か分かる

下のように様々な長さの2進数があったとします。

• 10010101
• 111001111010110
• 10110
• 10000010001110

これら数値が偶数なのか奇数なのかは1桁目を見るとすぐに分かります。

1桁目が「0」だと偶数で「1」だと奇数です。

理由は、

2桁目以降は必ず2の累乗なので偶数になります。

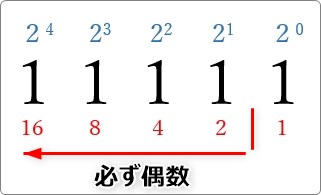
そうなると1桁目が「0」か「1」かによって偶数と奇数が変わることになります。

選択問題などで、簡単に不正解を省くことができるかもしれませんよ。

キリの良い桁数の数値は暗記しておく

2進数の累乗は、10進数へ変換する時以外でも使用します。

コンピュータに関する様々な内容で必要になることがあります。
また、組み合わせの数を算出する問題でもよく見かけます。

そのため、キリの良いビット数の最大値は覚えておいた方が良いでしょう。

ビット数	最大値
4	15
8	255
16	65535
24	約1677万
32	約43億

 

特に4ビットと8ビットの最大値は暗記しておくのがおすすめです。

練習問題

◎ 各問題をクリック(タップ)すると答えが出てくるよ