Introduction
2進数でマイナス(負数)を表現する方法を説明します。
コンピュータは「0」と「1」しか扱えないので、マイナスという概念がありません。
そこで一工夫することでマイナスを表現します。
2進数を学ぶ上で難しく感じる箇所の1つかもしれません。ゆっくり読み進めてください。

このページでの説明を理解するには下の3つの知識が必要です。
- 2進数への理解
- 2進数と10進数の相互変換
- 2進数の加算方法
不安な方は先にこれらの説明を見ていただくのがお勧めです。





一工夫ってどんな工夫なのかな
なぜマイナス表現を使うの?
最初に、なぜマイナス表現が必要なのかをハッキリさせておきましょう。
そもそもコンピュータは「0」と「1」しか扱えません。マイナスの数値は最初から「何それ?」っていう感じ。
そのため、「これはマイナスだよ」とコンピュータが分かるようにする必要があります。
また、演算処理では足し算しか使えません。
引き算も無理やり足し算にして計算しています。その際にマイナスの表現が必要になるのです。
ん?引き算を足し算?意味が分からない。

引き算を足し算にするってどういうこと?
例えば 9-3 の計算をしたかったとします。
9-3 を 9+(-3) として考えるのです。
9+(-3) → 9-3
になりますね。
※プラスとマイナスの組み合わせはマイナスになる
うん。引き算が足し算になりました。
この方法を使うには、 3 を -3 に変換する必要があります。
マイナスが確かに必要ですね。
コンピュータでのマイナス表現
では、コンピュータがどうやってマイナスを表現しているか説明していきます。
今回は4桁(4ビット)の2進数を例とします。
![]()
4ビットで「-1」を表現するには、まず、それよりも1ビット長い最小の数を「0」と考えます。
4ビットより1ビット長いのは5ビット。
その5ビットの最小の数は・・・。
えーと・・・。
(10000)2
ですね。
これを「0」として考える。
「-1」はこの数より「1」小さいということになりますね。
(10000)2 から 1 引くと・・・
(1111)2 になります。
「-2」の場合は、1111 から、さらに 1 引いて
(1110)2
「-3」の場合は、1110 から 1 引いて
(1101)2
この流れです。言葉で説明すると分かりにくいかもしれません。
まとめたのが下の図です。
大切な部分なので、「そうなんだ」となるまで見つめてください。

このような形でマイナスの数を表現します。
さて、マイナスだけではなくプラスの数も必要なので、4ビットを半分ずつ使用してプラスとマイナスを表現したのが下の表です。
2進数と10進数が対応しているので見比べてください。
「0」を境にして、左側がマイナスです。「1111」から「1」ずつ減らしていきます。
「0」を境にして、右側がプラスです。普通に「1」ずつ足していきます。
マイナスとプラスが被らないように、それぞれを増やしていきます。
4ビットは 24 の種類を表現できます。24 は 16 です。16種類を表現したところで終了。
※nビット使用した時に表現できる数が 2n になる話はこちらから。
さて、ここで注目したいのが、最上位ビット(左端のビット)です。
負を表現した場所は「1」になって、正を表現した場所は「0」になっていますね。
ということは、最初の1ビットを見ると正か負か分かる!
この正と負を区別する最上位ビットのことを「符号ビット」と呼んでいます
- 先頭の1ビットが「0」のとき・・・正
- 先頭の1ビットが「1」のとき・・・負

正か負かは左端の符号ビットで判断できるんだ~
先ほどの表で確認できますが、4ビット使用してマイナス表現をすると最大値と最小値は以下のようになります。
- 最大値・・・7
- 最小値・・・-8

マイナス表現無しだと、4ビットの最大値は 24-1 で、「15」まで表現できるのですが約半分になってしまいます。
※nビット使用した時の最大値は 2n-1 になる話はこちらから。
マイナス表現をすると、プラスとマイナスそれぞれ半分ずつ使用することにる。
これはしっかり覚えておきましょう。
そうそう。
「目の前にある2進数が最上位ビットを符号として扱うマイナス表現なのかどうか、どこで判断すれば良いの?」
と思った方もいるのでは。
試験で「2進数のマイナス表現」を問題にするときは、問題文に「最初の1ビットは符号として扱う」とか、「2の補数表現で表現された」などの言葉で分かり易く書いてあります。安心してください。
※「2の補数」という言葉が突然でてきましたが、これはこの後で説明します。
見ただけでは判断できないので問題文から読み取りましょう。

マイナス表現の2進数を扱うときは、そのことが問題文に書いてあるんだね
マイナスの数を簡単に求める方法
コンピュータでマイナスを表現する仕組みはここまでに説明した通りなのですが、
例えば10進数の (-55)10 を2進数のマイナス表現に変換したかった時はどうすればよいのでしょう。
8ビット使えるとして考えてみましょう。
まず、55を2進数に変換すると (00110111)2
※10進数を2進数へ変換する方法はこちらから。
これより1桁多い 9ビットの(100000000)2 を「0」として考えるから、
(11111111)2 が「-1」で (11111110)2 が「-2」で (11111101)2 が「-3」で・・・。
という感じで1ずつ減らして「-55」まで追っていくと大変ですね。

やってられないよ
そこで2の補数が登場します。
2の補数を使用すると簡単に2進数のマイナスを求めることができるのです。
ここでは、2の補数そのものの詳しい説明は長くなるので省きます。
2の補数とは簡単にいうと、その数を補うと次の桁の最小値になる数のことなのですが、詳しくは下のリンク先をご覧ください。

2の補数の求め方
2の補数に関する詳しい説明は、先ほどのリンク先で詳しく説明しているので、ここでは2の補数の求め方を簡単に説明しておきます。
2の補数を求めるのは難しくありません。
これだけです。
大きい数だと分かり難いので、とりあえず10進数の (5)10 を4ビット使用する例で考えてみましょう。

(1011)2 になりました。

これが「-5」になってるの?本当かな?
下の表をご覧ください。

「-5」の場所の2進数は「1011」になっていますね。
ちゃんとマイナス表現に変換されています。
先ほどの例 (55)10 をマイナス表現(2の補数)にしたかった場合も試してみましょう。
- とりあえず2進数に変換
- 全てのビットを反転する
※ビットの反転とは「0」→「1」、「1」→「0」にすること - 1を足す
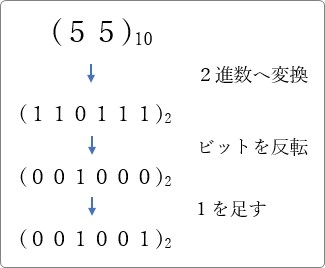
答えは (001001)2 となります。

ビットを反転して1足せばマイナスになるんだ
引き算を足し算で計算する?
今回の説明の始めの方に、「コンピュータは引き算も足し算として計算している」という話をしました。
例えば 9-3 であれば、9+(-3) として考えるという話です。
これを実際に2の補数を利用してやってみましょう。
「3」をマイナス表現の2の補数に変換してから計算します。
まず、「9」を2進数に変換すると (1001)2 です。
これはいったん置いておいて・・・
「3」を「-3」にするため2の補数を求めます。
- 「3」を2進数へ → (0011)2
※桁数は「9」を2進数へ変換した際の4桁に合わせます - ビットを反転 → (1100)2
- 「1」を足す → (1101)2
ということで、「3」の2の補数は (1101)2 になりました。
では、「9」の (1001)2 と「3」の2の補数 (1101)2 を足し算してみましょう。
9-3=6 なので答えが「6」になればOKですね。
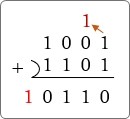
あれ?「22」になってしまった。
いや、この方法を使用するには以下のルールがあります。
このルールに沿って、一番左の「1」を無視すると、

「6」になります。
9-3=6
確かに、引き算を足し算で行うことができました。
慣れるために、もう一回やっておきましょう。
今度は 100-90 の計算を2の補数を使用してやってみます。
100+(-90) という感じ。
まず、「100」を2進数に変換すると (1100100)2 。
これはいったん置いておいて・・・。
次に「90」を「-90」にしたいので、2の補数を求めます。
- 「90」を2進数へ → (1011010)2
- ビットを反転 → (0100101)2
- 「1」を足す → (0100110)2
「90」の2の補数は (0100110)2 になりました。
では、それぞれを足してみましょう。
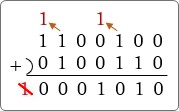
答えは「10」です。
100-90=10
合っていますね。

先頭ビットの桁上げを無視するのがポイントみたいだね
押さえておきたいポイント
- コンピュータは引き算を足し算として演算する
- 2進数でのマイナス表現では1桁大きい数字を「0」と考える
- 正負を判断する先頭ビットを符号ビットとよぶ
- 符号ビットは「0」が正、「1」が負
- マイナス表現を使用するときは、使える正負の数字は半分になる
- 2の補数を使用すると簡単にマイナスを求めることができる
- 2の補数を求めるには全てのビットを反転して「1」を足す
練習問題
◎ 各問題をクリック(タップ)すると答えが出てくるよ

必ず補数の説明もセットで読んでおいてね