Introduction
2進数での加算と減算のやり方をなるべく丁寧に説明します。
基本は普段から使用している10進数の足し算と引き算と同じです。足し算は繰り上げ(桁上げ)、引き算は繰り下げ(桁借り)をしますよ。
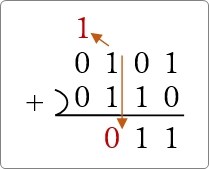

引き算はちょっと慣れが必要かもしれないよ
2進数を加算するやり方
2進数の計算も、10進数の計算をするときと基本は同じです。
例えば、普段使用している10進数で 620+593 の答えを知りたかったとします。
紙があれば、こう計算しますね。
まず、並べて書いて、
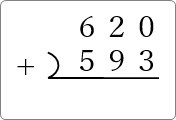
縦方向に計算して、桁が上がらない場合は、そのまま足し算して下に書きます。
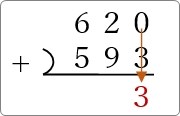
もし「10」以上になれば繰り上げが必要になります。
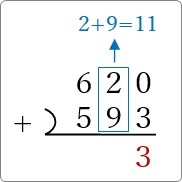
「11」になったときは、
繰り上がりの「1」を左上に書いて、残り(1桁部分)を下に書きます。
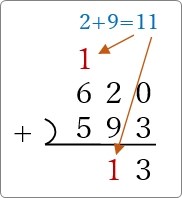
続けて次の桁を縦に足し算して、
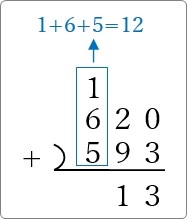
同じように「10」以上になって繰り上げが必要になったら、
左上に繰り上げの「1」を書いて、1桁部分の値を下に書く。
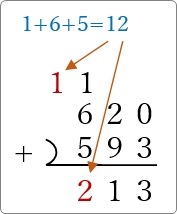
最後は繰り上げた「1」と下の部分(今回は無し)を足して計算終了。

桁が多いときは、こんな感じで足し算をしているはずです。
2進数での足し算も基本的な考え方は同じです。
しかし、10進数は1桁で扱えるのは「9」まで。「10」になったら繰り上げます。
一方、2進数は1桁で扱えるのは「1」まで。「2」になっただけですぐに繰り上げです。
- 10進数 → 10の大きさになると繰り上げる → 次の桁に「1」追加する
- 2進数 → 2の大きさになると繰り上げる → 次の桁に「1」追加する
言葉にするとイメージが浮かばないかもしれませんね・・・。
実は、2進数の計算はあまり難しく考えず、機械的にやり方を覚えてしまうのがお勧めです。
(11001)2 + (11010)2
の計算を例にルールを説明しますね。
やはり縦に並べて計算していきます。

縦の2つの2進数をそれぞれ処理していきますが、こう覚えましょう。
- 「1」と「0」が並んだ場所は「1」にする
※1+0 は 1ですよね
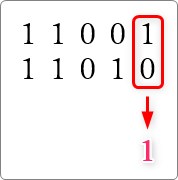
- 「0」と「1」が並んだ場所も「1」にする
※0+1 も 1ですよね
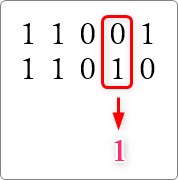
- 「0」と「0」が並んだ場所はそのまま「0」にする
※0+0 は 0ですよね
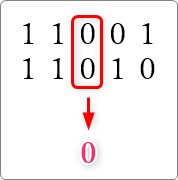
- 「1」と「1」の場所は「0」にして、繰り上げの「1」を左上に追加する
※1+1 は 2ですよね。2は2進数で表現すると「10」になるので、左の1を繰り上げに使って、右の0を下に書くイメージです。
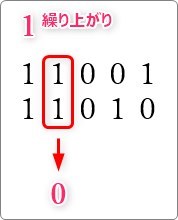
「1」が2つ並んだ場合は繰り上がりと覚えておきましょう。
まとめると、
- 「0」と「0」の場合は「0」 0+0=0
- 「0」と「1」の場合は「1」 0+1=1
- 「1」と「0」の場合も「1」 1+0=1
- 「1」と「1」の場合は「0」で繰り上げの「1」を追加 1+1=0 1繰り上げる
このルールを基に、次の足し算を計算してみましょう。
(0101)2 + (0110)2
※4桁の方が見やすいので頭に「0」をつけています。
まず、並べて準備します。
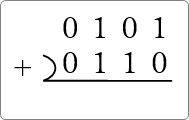
右側から計算していきます。
最初は「1」と「0」なので「1」ですね。
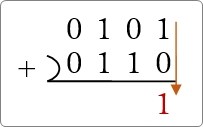
次は、「0」と「1」なのでやっぱり「1」
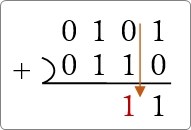
その次は「1」と「1」なので、「0」を下に書いて、繰り上げの「1」を左上に。
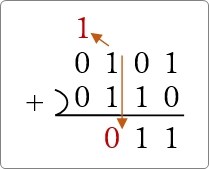
最後に繰り上げた「1」を下ろして、
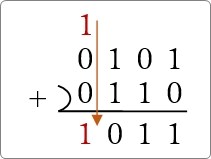
計算終了です。
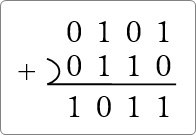
もう1問やってみましょう。
(01100010)2 + (00110011)2
にチャレンジです。
まず、並べて書いて準備して・・・。
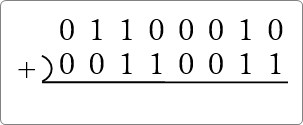
右側から処理していきます。
「0」と「1」の場合「1」ですね。

次の場所、「1」と「1」のときは繰り上げが必要なので、「0」を下ろして左上に繰り上げの「1」。
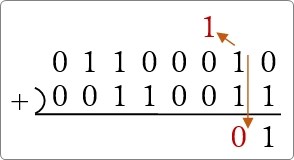
1+0+0=1 なので、そのまま「1」を下ろして、
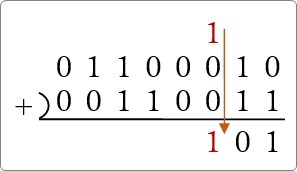
次の場所は「0」しかないので、そのまま「0」。
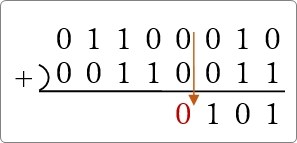
「0」と「1」のときは「1」を下ろして、
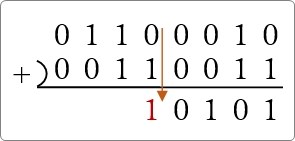
「1」と「1」のときは繰り上げが必要。
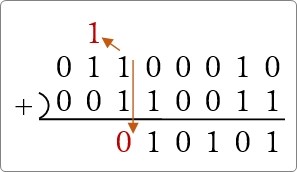
次の場所も繰り上げの「1」と、もとの「1」があるので、繰り上げになります。
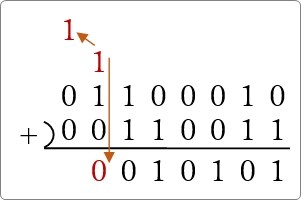
最後に繰り上がった「1」を下ろして
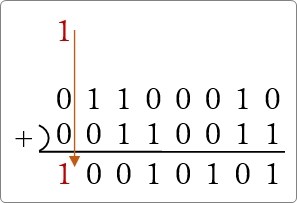
計算終了です。
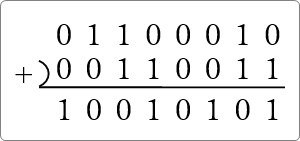
どうでしょうか?
「1」が並んでいるときだけ注意すればスムーズに進めることができるのでは。
繰り上げが連続することもあります。つまり「1」が3つ存在するパターンです。
下の例を参考にしてください。
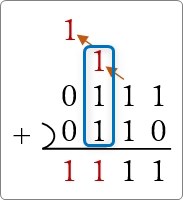
順番に書くと、下の青枠で囲んだ2つの「1」と「1」で繰り上げの「1」と「0」になり、
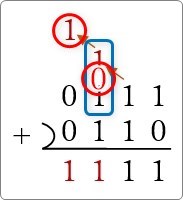
その「0」と1番下の「1」をセットで考えて、「1」を下ろします。
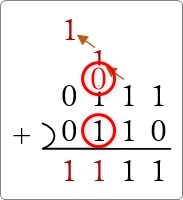

慣れてくると、あっという間に計算できるようになるよ
2進数を減算するやり方
2進数の減算も、10進数のやり方と考え方は同じです。
例えば普段 30-18 を計算をするときは、下のように準備して、
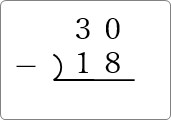
上の数字が足りない時は、左から「10」借りてきて計算しますね。
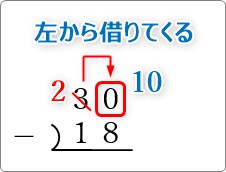
10-8=2 だから「2」
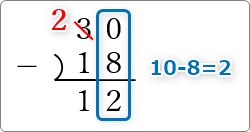
という感じ。
一方、2進数は借りてくるときの値は「10」ではなく「2」になります。
2進数は、1桁の大きさが2の累乗になっているのが理由です。
ん?と思った人は、難しいことは考えずに、
と単純に考えてしまいましょう。
- 10進数 → 引き算する数字が足りないときは、左の桁から10を借りてくる
- 2進数 → 引き算する数字が足りないときは、左の桁から2を借りてくる
「2」を借りてくる!
これだけ覚えておけば良いのですが、その「2」を借りる時の書き方にコツがあります。
縦に「1」を2つ並べる!
(10)2 – (01)2 を例にすると、下のようになります。
左から借りてくるときに「2」と書かずに「1」を2つ縦に並べます。
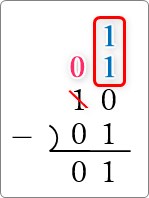
そして、下の2つの「1」を引き算してなくしましょう。
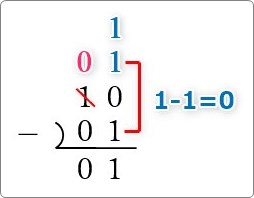
1番上の「1」が残りました。
それを下ろしてきます。
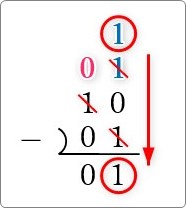
ちなみに、桁を借りてきた場所は必ず「1」が残ります。
※縦に「1」が3つあったら「1」と覚えても良いですね。
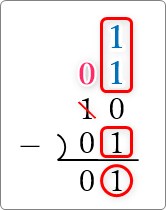
加算と同じようにまとめておきます、
- 「0」と「0」の場合は「0」 0-0=0
- 「0」と「1」の場合は「2」を左から借りてきて「1」を2つ縦に並べて減算後「1」残る 「2」 を桁借りして1-1=0で1残る
- 「1」と「0」の場合は「1」 1-0=0
- 「1」と「1」の場合は「0」 1-1=0
では、このやり方を頭に入れたら、計算にチャレンジです。
(1101)2 – (0010)2 をやってみましょう。
まず並べて書いて準備して、
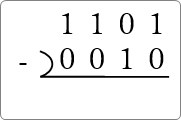
右側から進めていきます。
「1」-「0」で、「1」をそのまま残します。

次の場所は上が「0」なので桁借りが必要です。
借りた「1」を2つ縦に並べて書いて、左の借りた「1」を消して「0」にしておきましょう。
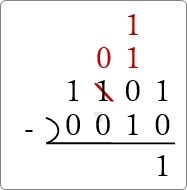
借りた「1」と最初の「1」を消して、借りたもうひとつの「1」を残します。
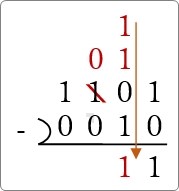
次の場所は桁を貸した「0」と、もとからある「0」になるので、そのまま「0」。
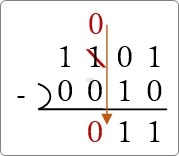
最後は、そのまま「1」を下ろして「1」。
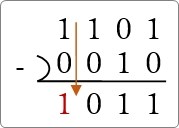
これで計算終了です。
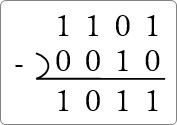
慣れるために、もう1問やってみましょう。
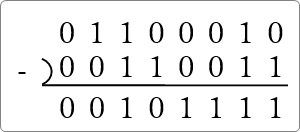
(01100010)2 – (00110011)2
まず準備して、
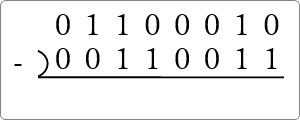
最初から、桁借りが必要になります。
左から桁借りして「1」を縦に並べて、「1」を下ろします。

次の場所が大変です!
先ほど桁を渡してしまったので「1」が「0」になってしまっています。
また左から桁を借りる必要がありますが、連続して「0」が並んでいるので、かなり離れた場所から借りてくることになります。
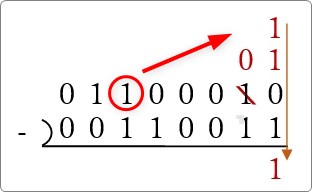
順番を追ってゆっくり作業していきます。
まず、左から3番目の「1」をもらって、右側に「1」を縦に並べます。
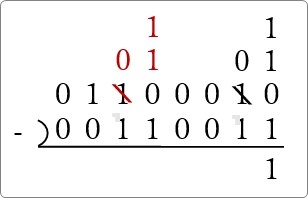
また右側に移動するために2つもらった「1」を1つだけもらいましょう。
※「1」を1つ消して、右に2つ「1」を追加
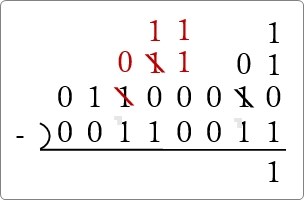
さらに右に移動するために同じように1つだけ「1」をもらいます。
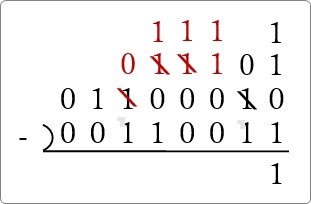
もう一回同じ作業が必要ですね。
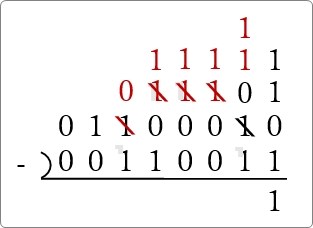
これで準備ができました。
「1」が3つあるので、「1」だけ下ろしてきましょう。
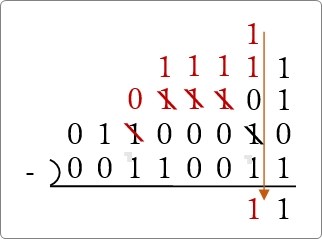
次の場所です。
「1」だけ残っているので、そのまま下ろします。
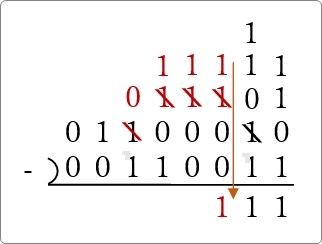
次も、そのまま下ろします。
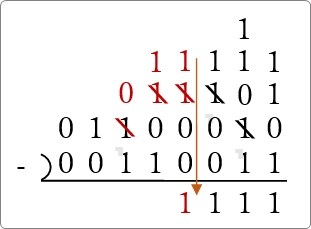
「1」-「1」なので「0」ですね。
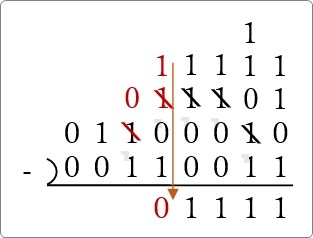
次の場所は「0」「1」なので桁を借りる必要があります。
桁を借りて「1」を下ろします。

最後の2つは、全部「0」があるだけです。
そのまま「0」にすれば計算終了。

長かったですね。
答えは (00101111)2 になりました。
離れた場所から借りてくるときに注意が必要です。
2つ書いた「1」の片方だけ消していきますよ。

長かったなー
押さえておきたいポイント
- 加算は「0」と「1」の組み合わせの結果を覚えておく
- 減算は繰り下がりで借りてくる際に「1」を2つ縦に書くようにする
- 減算で「1」が縦に3つあったら、「1」になる
練習問題
◎ 各問題をクリック(タップ)すると答えが出てくるよ
次の計算をやってみよう!
他の練習問題は下のリンク先から。


減算のときは、桁借りするときに注意だね

