Introduction
10進数の小数を2進数へ変換する方法を説明します。
小数点以下は、割り算ではなく掛け算を使って変換していきますよ。

また、今回の説明は浮動小数点数を学習する際にも使用します。
問題としての出題率は高くないかもしれませんが、覚えておくのがおすすめです。

浮動小数点数を理解する時にも必要みたいだね。
10進数の小数を2進数へ変換する方法
今回は、10進数 (7.3125)10 を2進数へ変換してみます。
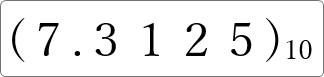
小数点を境に、左側の整数部分と右側小数点以下の部分を別々に処理していきましょう。

まずは左側の整数部分。
左側は通常の10進数を2進数へ変換する方法を使います。
今回の例では「7」を「2」で割りながら余りを右に記入して下から並べます。
※10進数から2進数へ変換する方法が苦手な方はこちらをご覧ください。
問題は右側の「0.3125」ですね。

こちらは、小数部分が「0」になるまで「2」を掛けていきます。
桁が上がって整数部分に「1」がきても、次の掛け算は小数部分だけ「2」を掛けます。
言葉にすると分かり難いので下の式を眺めてください。
- 0.3125×2 = 0.625
- 0.625×2 = 1.25
- 0.25×2 = 0.5
- 0.5×2 = 1.0
小数部分「0.315」に2を掛けて「0.625」、
その「0.625」に2を掛けると「1.25」になりますが、
「1」は置いておき、次は「0.25」に2を掛けます。
同じ流れで「2」を掛け算していき、計算結果が「1.0」(小数部分が0)になるまで進めます。
そして、計算結果の1桁目(下の赤字にした部分)を上から並べれば変換終了!
- 0.3125×2 = 0.625
- 0.625×2 = 1.25
- 0.25×2 = 0.5
- 0.5×2 = 1.0
今回の小数点以下の数値は「0101」となります。
今説明したのをまとめたのが下の画像です。
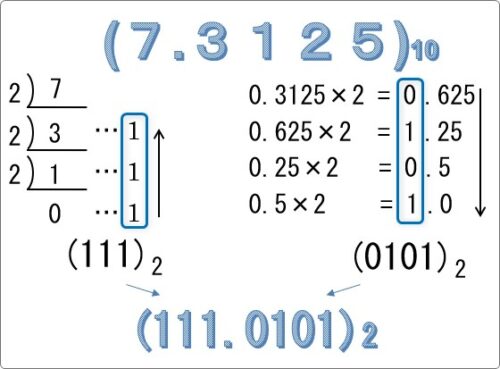
今回の10進数 (7.3125)10 を2進数へ変換すると (111.0101)2 になりました。
では、確認のためにもう一問やってみましょう。
(13.375)10 を2進数に変換します。

まず、小数点の左側の整数部分から処理していきましょう。

2で割り算していき、余りを右に記入して下から並べます。
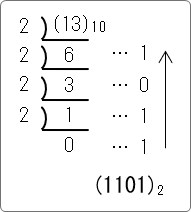
結果は (1101)2 になりました。
続いて小数点の右側です。

- 0.375×2 = 0.75
- 0.75×2 = 1.5
- 0.5×2 = 1.0
今度は上から並べると (011)2 になります。
そして、2つを繋げて
(1101.011)2 が変換後の結果です。

小数点以下を変換する方法は「2を掛ける」と覚えておく必要がありますね。

桁上げがあったら、次は「1.・・」じゃなくて「0.・・」にして計算する必要があるんだな
押さえておきたいポイント
- 小数点を境にして別々に考える
- 小数点の左側は通常の方法で2で割っていく
- 小数点の右側は「2」を掛けていき、桁上がりした場所の「1」、桁上がりが無い場所の「0」を上から並べる
- それぞれの結果を繋げる
練習問題
◎ 各問題をクリック(タップ)すると答えが出てくるよ
次の10進数を2進数に変換してみよう!

小数点以下の方は上から並べるよ


