Introduction
2進数のマイナス表現では2の補数を使用します。そもそも「補数」って何だろう?
これを解決しましょう。
教科書でも説明を簡略化してることが多いので、「なんとなく」の理解でやり過ごしている方も多いのでは・・・。
このページは、「補数」そのものの説明が中心となります。
- なぜ補数を使うの?
- 補数を使った計算方法は?
これらは下のリンク先で詳しく説明します。


少し長くなるみたい。張り切っていこー!
補数については2進数での負の数を表現する際の方法「ビット反転して1を足す」だけ覚えておけば十分かもしれません。
でも、「補数とはどういうものか。なぜそれを使用するのか」が文章問題として出題される可能性もあるので余力があれば押さえておきたい内容です。

「補数」って普段使わないからピンとこないよね
補数とは
補数とは、その数を補うと次の桁の最小値になる数、もしくはその桁の最大値になる数のことです。
どちらも「補数」とよびます。

補数には2つあるんだね
例えば (1010)2 の2進数を例にすると、
1つ高い桁の最小値は (10000)2 になり、その桁の最大値は (1111)2 になりますね。
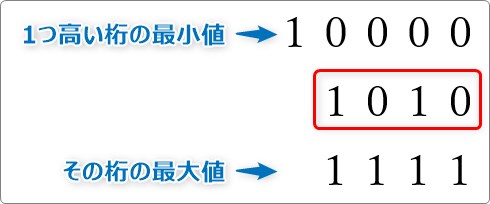
それぞれの値にするために「おぎなう数」が補数です。

補う数だから「補数」ということか
元の値にいくつ補う(足す)と1つ高い桁になるか、いくつ補う(足す)とその桁の最大値になるかを考えることになります。
2進数の場合は、前者を「2の補数」とよび、後者を「1の補数」とよびます。
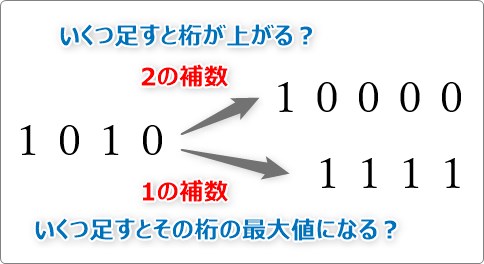
今回の例 (1010)2 での2の補数は (0110)2 となり、1の補数は (0101)2 です。
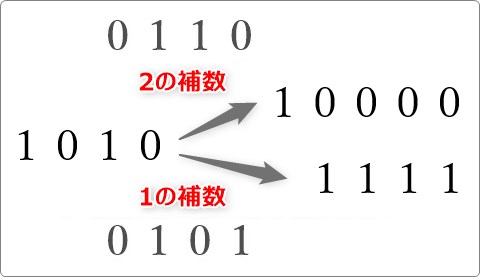
それぞれ足し算すると。 (10000)2 と (1111)2 になります。

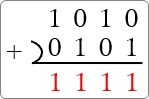
「補数」は2進数で使用されることが多いですが、他の〇進数でも考えることができます。日常で使用している馴染みのある10進数で考えてみましょう。
10進数のときには、10の補数と9の補数が存在します。
「10の補数」は、その数を補うと次の桁の最小値になる値です。
例として、「91」という数字で考えてみましょう。
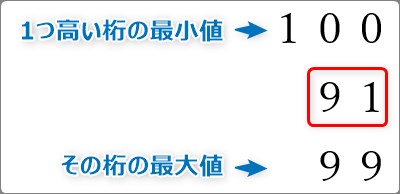
「91の10の補数は?」と聞かれたら、91にその値を足すと100に桁が上がる数です。
答えは「9」です。
91+9=100
次に「91の9の補数は?」と聞かれたら、91にその値を足すと99になる値です。
答えは「8」です。
91+8=99
もう気付いたか方もいるかもしれませんが、「1の補数」に「1」を足すと「2の補数」なりますし、「9の補数」に「1」を足すと「10の補数」になります。

「1の補数」と「2の補数」は「1」しか変わらないのか
ここで、2進数の時は「2の補数」と「1の補数」があって、10進数の時は「10の補数」と「9の補数」があるんだ。そもそも、なんでそう呼ぶの?と疑問に思った方もいるでしょう。
その理由を説明しておきます。
最初に以下のように説明しました。
例えば (1010)2 の2進数を例にすると、下の図のイメージでしたね。

両方が「補数」なのですが、こちらを分けてよぶ際はもともとは以下のように言います。
- その数を補うと次の桁の最小値になる数・・・基数の補数
- その数を補うと前の桁の最大値になる数・・・減基数の補数
「基数」とは〇進数の〇部分のこと。10進数のときは10で、8進数だったら8の部分のこと。
今の例は2進数なので「基数の補数」は「2の補数」と言い換えられます。
「減基数の補数」は「基数」から「減」するので「2」から「減」して「1の補数」と呼びます。
10進数だったら「基数の補数」は「10の補数」になり「減基数の補数」は「9の補数」になる。
どうでしょう。スッキリしたでしょうか。
以上が「補数」の説明です。
では、なぜその補数を今学習しているのか。
その理由は「2の補数」が2進数でのマイナス表現になるからです。
その話は別のページで説明したいと思います。
簡単に言うと「コンピュータで、引き算を足し算として行う際に利用される」ということなのですが、先に「2の補数」を簡単に求める方法をマスターしておきましょう。
2の補数の求め方
コンピュータで、引き算を足し算として行う際に利用される「2の補数」ですが、簡単に求めることができます。
ちなみに「2の補数」とは前述した説明をまとめると次のようになります。
例えば (1010)2 の「2の補数」を聞かれたら、(1010)2 にいくつ補えば次の桁の (10000)2 になるかを考えます。


いくつ補えば次の桁の最大値になるの?
考え方としては、最初にその桁の最大値になる数を求めます。
2進数では「1」が全て並んだものがその桁の最大値です。
4桁であれば (1111)2 ですし、6桁の2進数であれば (111111)2 、8桁の2進数であれば (11111111)2 。
とにかく難しい事は考えずに「1」が全て並んでいれば、その桁の最大値なのです。
今回の例、(1010)2 であれば、これを (1111)2 にすればよいのですが、これまた簡単。
それぞれの「1」「0」を逆にする(反転する)だけで終わります。
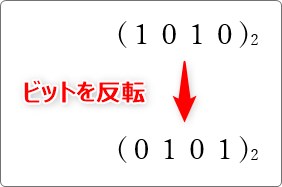
全てを「1」にしたいわけですから、「0」の場所を「1」にしたものを足せばよい。
言われてみると当たり前のはなしです。

ということで、ビットを反転した数が、その桁の最大値にするための数になることが分かりました。
ちなみに、これって「1の補数」です。
そのままでは、 (1111)2 で「1の補数」のままなので2の補数 (10000)2 にするためには「1」足す必要があります。
ということで、(0101)2 に「1」足して、(0110)2 が (1010)2 の2の補数になります。
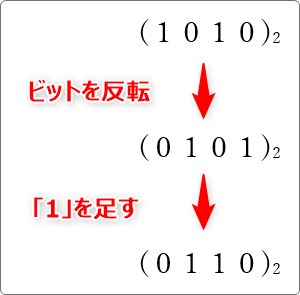
さて、確認です。
(1010)2 に (0110)2 を足すと (10000)2 になればOKです。
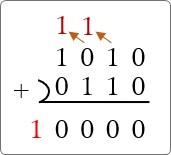
うん。大丈夫そうです。
※2進数の足し算の方法はこちらから。
もう一回、他の例でやってみましょう。
今度は (100110)2 の2の補数を求めてみます。
まず、ビットを反転します。
「1」を「0」へ、「0」を「1」へ。
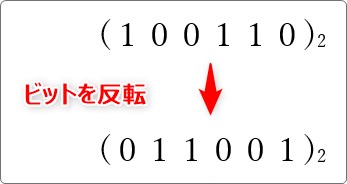
(1011001)2 になります。
この数に「1」足します。
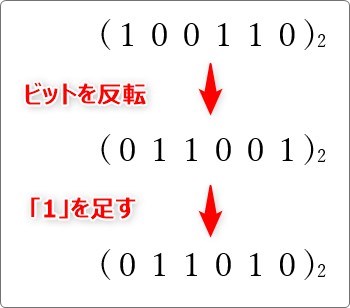
結果は (011010)2 です。
2つを足すとちゃんと、次の桁の最小値 (1000000)2 になるか確認してみます。
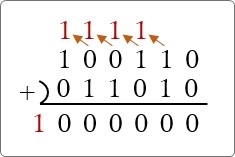
うん。ちゃんと桁上げが続いて (1000000)2 になりますね。

2進数の足し算に慣れておくと楽だね
押さえておきたいポイント
- 補数とは、その数を補うと次の桁の最小値になる値、もしくは前の桁の最大値になる値のこと
- 補数には2つある(基数の補数と減基数の補数)
- 2の補数は2進数のマイナス表現で使用される
- 1の補数に「1」足すと2の補数になる
- 2の補数を求めるには全てのビットを反転して「1」を足す
練習問題
◎ 各問題をクリック(タップ)すると答えが出てくるよ
次の問題をやってみよう!
セットで下のリンク先も読んでおこう


言葉そのまま「補う数」なんだね

