２進数で「表現できる数は２n」と「最大値は２n-1」の違いをハッキリさせよう

Introduction

２進数やビット数に関係する公式に「2ⁿ」と「2ⁿ-1」があります。

この２つの違いを正確に理解していないと解けない問題を見かけることがあります。

ここでハッキリと違いを確認しておきましょう。

 

この場所を学習する前に、２進数を理解しておく必要があります。

下のリンク先で説明しています。

コンピューターで扱う２進数とは何？ーその意味を分かり易く説明しますー

コンピューターで扱う２進数とはどのようなものでしょうか。文系の方でも理解しやすいように、なるべく簡単にわかりやすく説明してみます。

prau-ict.com

 

2nと２n-1の違い

説明の前に、２進数の１桁を１ビットと呼ぶ事を再確認。

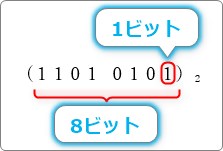
上の画像の場合は８ビット存在することになります。

 

では、はじめましょう。

まず、それぞれの式が何を算出するものなのかを確認しておきましょう。

ん？同じに見える。
いえ、赤字にした部分が違います。

「表現できる数」と「最大値」
この違いを認識するのが大切です。
※「表現できる数」は「表現できる組み合わせ」と言い換えることができます。

 

具体的な例として4ビットで考えてみましょう。

「4ビットで表現できる数は2⁴になる」
「4ビットで表現できる最大値は2⁴-1」

になるということです。
それぞれ計算してみると、

2⁴ = 16
2⁴-1 = 15

「4ビットで表現できる数は16になる」
「4ビットで表現できる最大値は15」

ということになります。

 

この違いをスッキリ理解するには少ないビット数で考えるのがおすすめです。

まず、1ビットで違いを確認してみます。

「1ビットで表現できる数は幾つありますか？」

１ビットにつき「0」と「1」が使えるので、表現できる数（組み合わせ）は2つですね。

では、

「1ビットで表現できる最大値は幾つになりますか？」

「0」と「1」しか使えないので最大値は「1」になりますね。

表現できる数は「2」で、最大値は「1」。
「1」の違いが存在します。

 

次に2ビットで考えてみましょう。

「2ビットで表現できる数は幾つありますか？」

下の画像を見てもらうように答えは「4」。
4つの組み合わせが可能です。

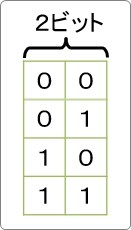
では、「2ビットで表現できる最大値は幾つになるでしょうか？」

全ての桁に「1」が存在する状態が一番大きい値です。
つまり、2ビットの最大値は「11」になります。

2進数を10進数に変換。

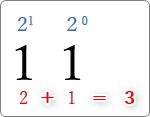
答えは「3」です。

表現できる数は「4」で、最大値は「3」。やはり「1」の違いが存在しますね。

 

もう一回だけいってみましょう。

「3ビットで表現できる数は幾つありますか？」

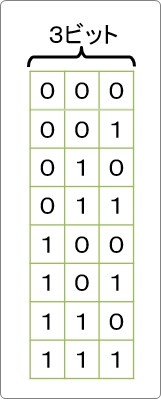
全部で8つの組み合わせが可能です。
8種類表現できるということですね。

では、「3ビットで表現できる最大値は幾つになるでしょうか？」

答えは「7」です。

表現できる数は「8」で、最大値は「7」。やはり「1」の違いが存在しますね。

 

どうやら「表現できる数」と「最大値」には「1」の開きがあるようです。

さて、この「1」の違いは何でしょうか。

 

これまで見たビットごとの「表現できる数」をまとめた画像を見てください。

それぞれ「2」「4」「8」の組み合わせが確かにありますね。

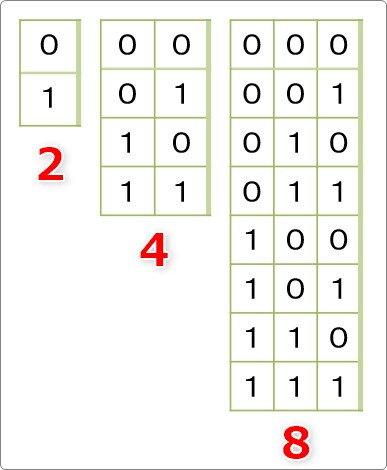
そして、「最大値」はここから「1」少なくなるわけです。

何が必要ないのでしょうか？

・・・

気付きましたか？

「0」ですね。

「0」とはそもそも数字の大きさが存在しない場所。値が存在しない場所です。

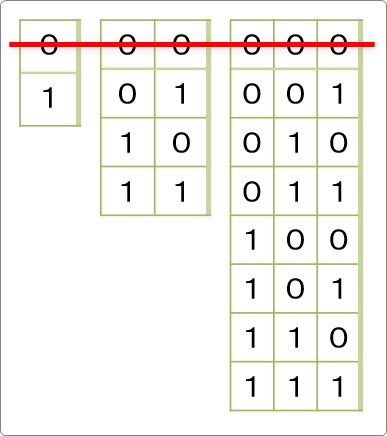
表現できる組み合わせとして「0」は入れるべきですが、最大値としては考える必要がないということです。

最大値は「0」の分を抜かして考える

「2n-1」の「-1」部分は「0」を省くためだと覚えておきましょう。

 

nビットで表現できる数、表現できる種類、表現できる組み合わせ
↓
2ⁿ

 

nビット使用した際の最大の値
↓
2ⁿ-1

 

と覚えておけば安心です。

 

言われて見ると単純な話ですね。

この単純な事をしっかり理解しているか、式の暗記で終わらせているかで応用問題を解く際に違いが出てきます。

練習問題

◎ 各問題をクリック(タップ)すると答えが出てくるよ