Introduction
情報の授業でも扱う浮動小数点数の説明です。
小数点の位置が決まっているものを固定小数点数とよぶのに対し、小数点の位置を固定せずにあらわした数を浮動小数点数とよびます。

小数点を固定しないで移動する?

コンピュータでは、2進法の浮動小数点数が使用されます。
浮動小数点数を利用することで、とても小さい数から大きい数まで広い範囲の数値を表現することができます。
扱う数値に応じて桁数を変えることでメモリの使用も抑えることができますし、浮動小数点の計算に特化したハードウェアもあり高速な計算が可能になっています。
演算処理が多い3Dゲームなどでは、この浮動小数点数の計算スピードが重要な要素となっていますよ。
「情報落ち」や「桁落ち」の誤差の問題も関係してきます。
変換の際には小数点を含んだ10進数を2進数へ変換する方法や、2進数の足し算の知識も必要になるのでじっかり読み進めてください。

頻繁に出題されないけど「誤差」を理解するためにも必要な知識だよ
浮動小数点数とは
まず、浮動小数点数がどういうものか、全体像を説明していきます。
浮動小数点数を使用するには、使用するビットを固定する必要があります。
例えば16ビットや32ビット64ビットというように。

今回は16ビットを例として説明していきます。
そして、その決められたビットを「符号部」「仮数部」「指数部」の3つに分けて小数点数をあらわします。
下の図がそのイメージです。
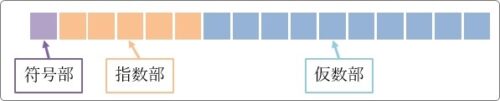
「浮動小数点数」という言葉をみたら、この3つに分かれるイメージが頭に浮かぶようにしておきましょう。
その浮動小数点数の3つの要素は以下のようになります。
- 符号部・・・常に最上位ビット(左端)。プラスかマイナスかを「0」か「1」で指定する
※「0」がプラス。「1」がマイナス。 - 仮数部・・・元の値を正規化した指数の値に使用ビットから1ビット少ない桁の最大値を足した数
- 指数部・・・正規化後の小数点以降の数値を左詰めにする
突然文字で説明されてもピンときませんね。
実際に10進数の実数を浮動小数点数に変換しながらゆっくり説明していきます。
浮動小数点数へ変換する方法
では、その流れを詳しくみていきましょう。
10進数の (2.5)10 を2進数の浮動小数点数にしてみます。
まず、 (2.5)10 を2進数に変換しなければいけません。
小数点の左側のプラス部分「2」を2進数にすると (10)2 。
小数点の右側のマイナス部分「0.5」を2進数に変換すると (1)2 。
2つを繋げると (10.1)2 になります。
小数点のある10進数を2進数へ変換する方法は下のリンク先を参考にしてください。

この (10.1)2 を浮動小数点数にしていきます。
下の3つに分けて順番に変換していきましょう。

まず、「符号部」です。
ここは簡単。
プラスの場合は「0」で、マイナスの場合は「1」を入れます。
今回はプラスなので「0」になります。
![]()
次が「指数部」。
ここは面倒です。
元の数値を正規化した指数部の値に使用ビットから1ビット少ない桁の最大値を足した数を入れます。

うーーーん、なんだか面倒そう
2つの数値を出して足し算しなければなりません。
「元の数値を正規化した指数部」を最初に求めてみます。
まず、変換する2進数の小数点をずらして、1.〇〇×2nの形にします。
※1番左に「1.」が来るように左に全体をずらしていく。
今回変換する2進数は (10.1)2 なので、小数点を左に1つずらすことで、 1.01×21 になります。
※ずらした回数が、2nのn部分になる。
そして、今変換した 1.01×21 の 1.01×21 の場所(指数部)を使用します。
今回の「元の数値を正規化した指数部」は「1」になります。
次に、使用ビットから1ビット少ない桁の最大値を求めます。
今回の「指数部」での使用ビットは下図のように5ビットです。

5ビットから1ビット少ない桁は4ビット。その最大値が必要となります。
4ビットの最大値は (1111)2 。これを使用します。
その (1111)2 と、正規化した 1.01×21 の赤文字部分「1」を足すのです。
1+1111 → 10000
ですね。
これが今回の指数部の値になります。
![]()
2進数の足し算が苦手な方は下のリンク先を参考にしてください。

最後に青部分の仮数部を求めましょう。
ここは簡単。
先ほど正規化した 1.01×21 の赤字部分を左詰めで使います。
青い部分を埋めていくと・・・。
![]()
これで完成です。
さて、これで説明は終わりですが、1度やってみただけでは不安ですね。
もう一つだけやってみましょう。同じだと面白くないので今度は32ビットの浮動小数点数に挑戦です。
10進数 (46.875)10 を2進数の浮動小数点数に変換してみます。
符号部1ビット、指数部8ビット、仮数部23ビットとします。

まず (46.875)10 を2進数に変換します。
結果は (101110.111)2 です。
では、符号部、指数部、仮数部を順番に埋めていきましょう。
- 符号部・・・常に最上位ビット(左端)。プラスかマイナスかを「0」か「1」で指定する
- 仮数部・・・元の値を正規化した指数の値に使用ビットから1ビット少ない桁の最大値を足した数
- 指数部・・・正規化後の小数点以降の数値を左詰めにする
符号部は正の数なので「0」になります。
![]()
次に仮数部です。
(101110.111)2 を正規化すると → 1.01110111×25
指数部の5を2進数に変換すると (101)2 です。
今回使用する指数部は8ビットなので、その1ビット少ない最大値は(1111111)2。
(101)2 + (1111111)2 → (10000100)2
指数部は「10000100」になります。
![]()
最後に仮数部ですが、正規化後の 1.01110111×25の小数点以降の数値を使うので
仮数部は「01110111」を左詰めで使います。
それらを3つを合体すると、
(01000010001110111000000000000000)2になります。
![]()
どうでしょう。
大切なのは途中の正規化ですね。
また、10進数から変換するときは小数点を含む数を2進数へ変換する知識が必要になります。
ちょっと大変ですが、うまく変換できると嬉しくなりますね。

思ったより大変だったかもー
押さえておきたいポイント
- 浮動小数点数は「符号部」「指数部」「仮数部」に分ける
- 小数点を移動する正規化が必要
- 符号部は「0」が正、「1」が負
- 「指数部」の求め方
- 「仮数部」の求め方
練習問題
◎ 問題をクリック(タップ)すると答えが出てくるよ
次の10進数を2進数の浮動小数点数にしてみよう!
※符号部、指数部、仮数部はそれぞれ、1ビット、5ビット、10ビットとする。
答え 0100110111111000

指数部の求め方を忘れちゃいそうだな・・・

